Numrat kryesorë, themelet e matematikës, kanë magjepsur për shekuj − tani teknologjia po revolucionarizon kërkimin për ta

Një copë kocke të butë të gdhendur me shenja të pashpërndara që datojnë 20,000 vjet mbrapa i habiti arkeologët derisa vunë re diçka unike – gdhendjet, vijat si shënues të numrave, mund të përfaqësonin numrat kryesorë. Në mënyrë të ngjashme, një tablë guri nga viti 1800 p.e.s. i shkruar me numra babilonas përshkruan një sistem numrash të ndërtuar mbi numrat kryesorë.

Si kocka Ishango, tabela Plimpton 322 dhe artefaktet e tjera gjatë historisë tregojnë se numrat kryesorë kanë magjepsur dhe kapur vëmendjen e njerëzve gjatë gjithë historisë. Sot, numrat kryesorë dhe vetitë e tyre studiohen në teorinë e numrave, një degë e matematikës dhe fusha aktive e kërkimit sot.

Një histori e numrave kryesorë

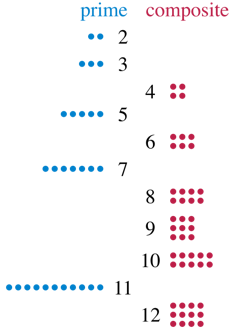
Në mënyrë jozyrtare, një numër pozitiv i numërimit më i madh se një është kryesor nëse ai numër pikash mund të rregullohet vetëm në një rrjet drejtkëndësh me një kolonë ose një rresht. Për shembull, 11 është një numër kryesor pasi 11 pika formojnë vetëm rrjete drejtkëndëshe me madhësi 1 me 11 dhe 11 me 1. Përkundrazi, 12 nuk është kryesor pasi mund të përdorni 12 pika për të bërë një rrjet prej 3 me 4 pika, me shumë rreshta dhe shumë kolona. Librat e matematikës përcaktojnë një numër kryesor si një numër i plotë më i madh se një që vetëm divisoret pozitive janë 1 dhe vetja e tij.

Historiani i matematikës Peter S. Rudman sugjeron që matematikët grekë mund të ishin të parët që kuptuan konceptin e numrave kryesorë, rreth vitit 500 p.e.s.

Rreth vitit 300 p.e.s., matematikani dhe logjiku grek Euclidi provoi se ekzistojnë pa fund numra kryesorë. Euclidi filloi duke supozuar se ka një numër të fundëm të numrave kryesorë. Pastaj ai krijoi një numër kryesor që nuk ishte në listën fillestare për të krijuar një kontradiktë. Meqenëse një parim themelor i matematikës është të jesh logjikisht i qëndrueshëm pa kontradikta, Euclidi përfundoi se supozimi i tij fillestar duhet të jetë i gabuar. Pra, ekzistojnë pa fund numra kryesorë.

Argumenti përcaktoi ekzistencën e numrave kryesorë pa fund, megjithatë ai nuk ishte veçanërisht konstruktiv. Euclidi nuk kishte një metodë efikase për të listuar të gjithë numrat kryesorë në një listë në rritje.

Në mesjetë, matematicienët arabë avancuan teorinë e grekëve për numrat kryesorë, të cilët gjatë kësaj kohe njihej si numra hasam. Matematikani persian Kamal al-Din al-Farisi formuloi teoremin themelor të aritmetikës, i cili thotë se çdo numër i plotë pozitiv më i madh se një mund të shprehet në mënyrë unike si një produkt i numrave kryesorë.

Nga kjo pikëpamje, numrat kryesorë janë blloqet bazë për ndërtimin e çdo numri të plotë pozitiv duke përdorur shumëzimin – të ngjashëm me atomet që bashkohen për të bërë molekula në kimikë.

Numrat kryesorë mund të klasifikohen në lloje të ndryshme. Në vitin 1202, Leonardo Fibonacci prezantoi në librin e tij “Liber Abaci: Libri i Kalkulimit” numrat kryesorë të formës (2^p - 1) ku p është gjithashtu kryesor.

Sot, numrat kryesorë në këtë formë quhen Numrat kryesorë Mersenne pas monakut francez Marin Mersenne. Shumë nga numrat kryesorë më të mëdhenj të njohur ndjekin këtë format.

Disa matematikanë të hershëm besonin se një numër i formës (2^p – 1) është kryesor sa herë që p është kryesor. Por në vitin 1536, matematikani Hudalricus Regius vërejti se 11 është kryesor por jo (2¹¹ - 1), që është 2047. Numri 2047 mund të shprehet si 23 herë 89, duke mohuar këtë supozim.

Ndërsa nuk është gjithmonë e vërtetë, teoricienët e numrave kuptuan se shkurtuesi (2^p - 1) shpesh prodhon numra kryesorë dhe jep një mënyrë sistematike për të kërkuar numra të mëdhenj kryesorë.

Kërkimi për numra të mëdhenj kryesorë

Numri (2^p – 1) është shumë më i madh në krahasim me vlerën e p dhe ofron mundësi për të identifikuar numra të mëdhenj kryesorë.

Kur numri (2^p - 1) bëhet mjaft i madh, është shumë më e vështirë të kontrollohet nëse (2^p - 1) është kryesor – pra, nëse (2^p - 1) mund të rregullohet vetëm në një varg të drejtë me një kolonë ose një rresht.

Fatkeqësisht, Édouard Lucas zhvilloi një test për numrat kryesorë në vitin 1878, i cili më vonë u provo nga Derrick Henry Lehmer në vitin 1930. Puna e tyre rezultoi në një algoritëm efikas për vlerësimin e potencialeve të numrave Mersenne kryesorë. Duke përdorur këtë algoritëm me llogaritje manuale në letër, Lucas tregoi në vitin 1876 se numri me 39 shifra (2¹²⁷ - 1) është 170,141,183,460,469,231,731,687,303,715,884,105,727, dhe ky vlerë është kryesor.

I njohur gjithashtu si M127, ky numër mbetet kryesori më i madh i verifikuar me llogaritje manuale. Ai mbante rekordin për kryesorin më të madh të njohur për 75 vjet.

Kërkuesit filluan të përdorin kompjuterët në vitet 1950, dhe shpejtësia e zbulimit të kryesorëve të rinj të mëdhenj u rrit. Në vitin 1952, Raphael M. Robinson identifikoi pesë kryesorë të rinj Mersenne duke përdorur një Kompjuter Standard Perëndimor Automatik për të kryer testet e numrave kryesorë Lucas-Lehmer.

Ndërsa kompjuterët përmirësoheshin, lista e kryesorëve Mersenne u rrit, veçanërisht me mbërritjen e superkompjuterit Cray në vitin 1964. Edhe pse ekzistojnë shumë kryesorë, kërkuesit nuk janë të sigurt sa prej tyre janë të tipit (2^p - 1) dhe janë kryesorë Mersenne.

Deri në fillim të viteve 1980, kërkuesit kishin grumbulluar mjaftueshëm të dhëna për të besuar me siguri se ekzistojnë kryesorë të pafundmë Mersenne. Ata madje mund të hamendësonin sa shpesh shfaqen këta numra kryesorë, mesatarisht. Matematicienët nuk kanë gjetur ende një provë, por të dhënat e reja vazhdojnë të mbështesin këto hamendësime.

George Woltman, një shkencëtar kompjuterësh, themeloi Great Internet Mersenne Prime Search, ose GIMPS, në vitin 1996. Përmes këtij programi bashkëpunues, kushdo mund të shkarkojë falas softuerin e disponueshëm nga faqja e GIMPS për të kërkuar numra kryesorë Mersenne në kompjuterët e tyre personalë. Faqja përmban udhëzime të veçanta mbi mënyrën e pjesëmarrjes.

GIMPS tani ka identifikuar 18 primë Mersenne, kryesisht në kompjuterë personalë duke përdorur bërthama Intel. Programi mesatarisht zbulon një të ri çdo një deri dy vjet.

Primri i njohur më i madh

Luke Durant, një programues i pensionuar, zbuloi rekord aktual për primrin më të madh të njohur, (2^136,279,841 - 1), në tetor 2024.

I referuar si M136279841, ky numër me 41,024,320 shifra ishte i 52-ti primri Mersenne i identifikuar dhe u gjet duke ekzekutuar GIMPS në një rrjet të disponueshëm publikisht rrjet kompjuterik në re.

Ky rrjet përdori bërthama Nvidia dhe funksionoi në 17 vende dhe 24 qendra të të dhënave. Këto bërthama të avancuara ofrojnë përpunim më të shpejtë duke trajtuar mijëra llogaritje në të njëjtën kohë. Rezultati është kohë më e shkurtër ekzekutimi për algoritme të tilla si testimi i numrave primë.

Fondacioni Elektronik Frontier është një grup i lirive civile që ofron çmime parash për identifikimin e numrave të mëdhenj kryesorë. Ai dha çmime në vitin 2000 dhe 2009 për një milion shifra të verifikuara dhe numra kryesorë me 10 milion shifra.

Sfida të ardhshme për entuziastët e numrave kryesorë të mëdhenj janë të identifikojnë numrat kryesorë të parë me 100 milion shifra dhe 1 miliard shifra. Çmimet EFF prej 150,000 dollarë amerikanë dhe 250,000 dollarë, përkatësisht, presin individin ose grupin e parë të suksesshëm.

Të tetë nga 10 numrat kryesorë më të mëdhenj të njohur janë numra kryesorë Mersenne, kështu që GIMPS dhe llogaritjet në re janë gati të luajnë një rol të dukshëm në kërkimin për numra kryesorë të mëdhenj rekord.

Numrat e mëdhenj kryesorë kanë një rol të rëndësishëm në shumë metoda enkriptimi në sigurinë kibernetike, kështu që çdo përdorues i internetit ka përfitim nga kërkimi për numra të mëdhenj kryesorë. Këto kërkime ndihmojnë në mbajtjen e komunikimeve dixhitale dhe informacionit të ndjeshëm të sigurt.

Kjo histori u përditësua më 30 maj 2025 për të korrigjuar emrin e matematicianit grek Euclid dhe për të korrigjuar faktorët e 2047.